Text operations in neural networks
Describing text operations and transformations in neural networks
Overview
Text operations in neural networks involve transforming text data into numerical representations that machines can process. These operations are fundamental to Natural Language Processing (NLP) tasks. The primary challenge is converting variable-length text sequences into fixed-size numerical representations while preserving semantic meaning and contextual relationships.
How Text Processing Works in Neural Networks:
Text processing typically follows a pipeline of operations: tokenization, embedding, and contextual encoding. Each step transforms the text into increasingly sophisticated representations that capture different aspects of language structure and meaning.
Why Use Text Operations?
Numerical Representation: Neural networks can only process numerical data, requiring text to be converted into vectors or matrices.
Semantic Preservation: Operations must maintain meaningful relationships between words and phrases while converting to numerical form.
Context Handling: Text operations need to capture both local (nearby words) and global (document-level) context.
Text Operations
Tokenization
Tokenization is the process of breaking text into smaller units (tokens) such as words, subwords, or characters. Different tokenization strategies exist:
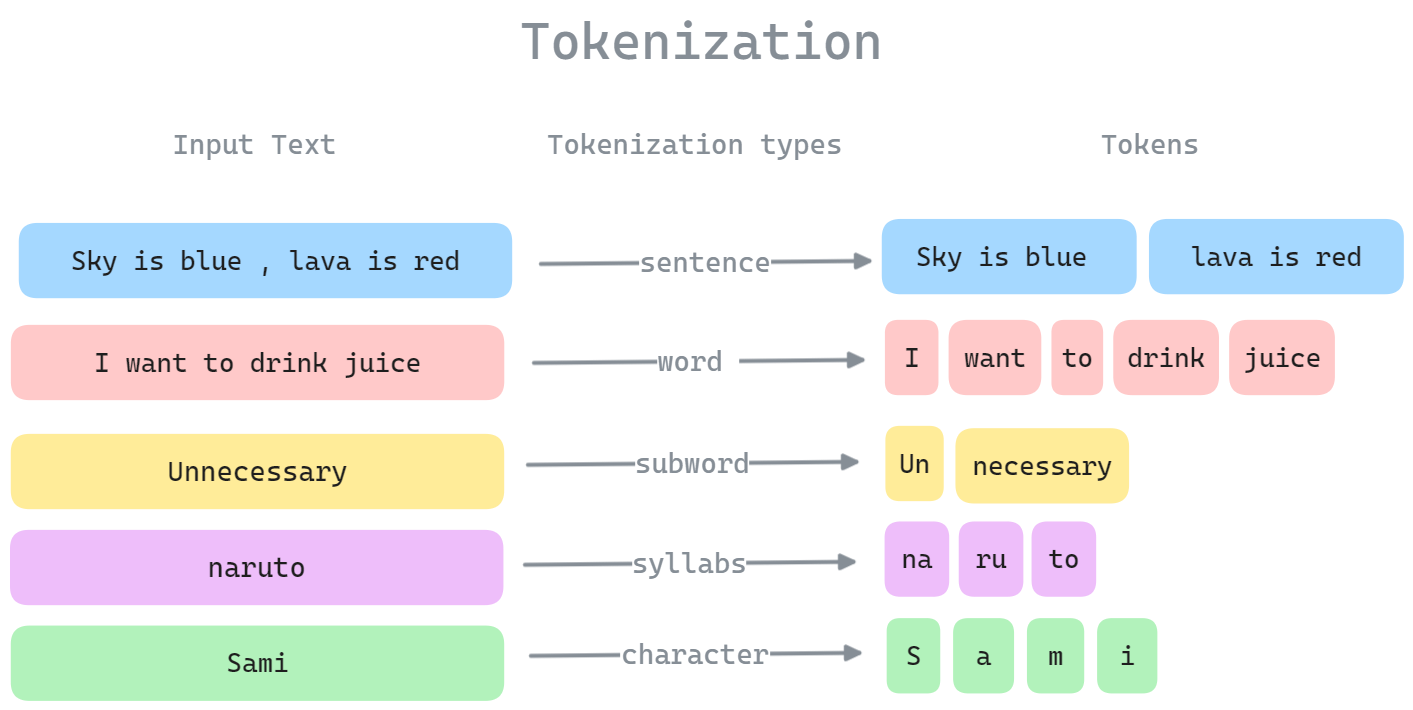
 Figure 1.0: Different tokenization strategies
Figure 1.0: Different tokenization strategies
BPE (Byte-Pair Encoding) Algorithm:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def learn_bpe(text, num_merges):
# Initialize vocabulary with characters
vocab = {c: text.count(c) for c in set(text)}
pairs = get_stats(vocab)
for i in range(num_merges):
if not pairs:
break
best = max(pairs, key=pairs.get)
vocab = merge_vocab(best, vocab)
pairs = get_stats(vocab)
return vocab
def get_stats(vocab):
pairs = {}
for word, freq in vocab.items():
symbols = word.split()
for i in range(len(symbols)-1):
pair = (symbols[i], symbols[i+1])
pairs[pair] = pairs.get(pair, 0) + freq
return pairs
def merge_vocab(pair, vocab):
new_vocab = {}
bigram = ' '.join(pair)
replacement = ''.join(pair)
for word, freq in vocab.items():
new_word = word.replace(bigram, replacement)
new_vocab[new_word] = freq
return new_vocab
Text Embedding
Text embedding converts tokens into dense vectors in a continuous vector space. The most common approaches are:
One-Hot Encoding:
For vocabulary size $V$, each word is represented as a vector of size $V$ with a 1 in the corresponding position:
\[\text{one\_hot}(w_i) = [0, \ldots, 1, \ldots, 0]\]Word Embeddings:
Learned dense vectors that capture semantic relationships. Given a word $w$, its embedding is:
\[\text{embed}(w) = W \cdot \text{one\_hot}(w)\]where $W$ is the embedding matrix.
Word2Vec Implementation:
1
2
3
4
5
6
7
8
9
10
class SkipGram(nn.Module):
def __init__(self, vocab_size, embedding_dim):
super(SkipGram, self).__init__()
self.embeddings = nn.Embedding(vocab_size, embedding_dim)
self.output = nn.Linear(embedding_dim, vocab_size)
def forward(self, x):
embed = self.embeddings(x)
out = self.output(embed)
return F.log_softmax(out, dim=1)
Positional Encoding
To capture word order in sequences, positional encoding adds position information to embeddings:
\(PE_{(pos,2i)} = \sin(pos/10000^{2i/d_{model}})\) \(PE_{(pos,2i+1)} = \cos(pos/10000^{2i/d_{model}})\)
Where:
- $pos$ is the position in the sequence
- $i$ is the dimension
- $d_{model}$ is the embedding dimension
1
2
3
4
5
6
7
8
9
def positional_encoding(max_seq_len, d_model):
pe = torch.zeros(max_seq_len, d_model)
position = torch.arange(0, max_seq_len, dtype=torch.float).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
return pe
Attention Mechanism
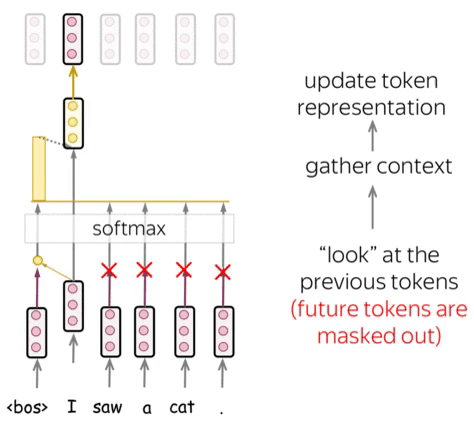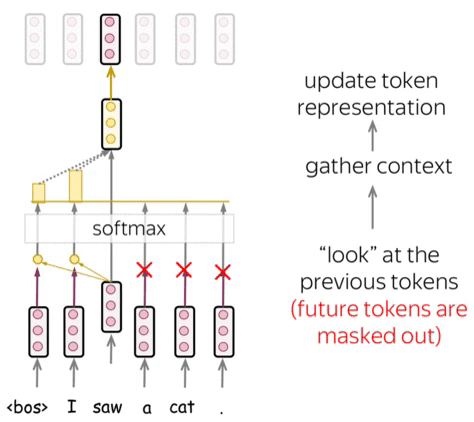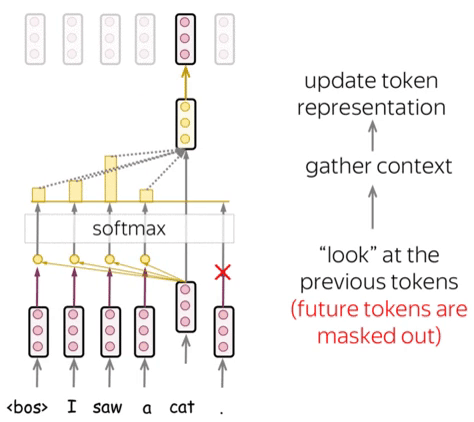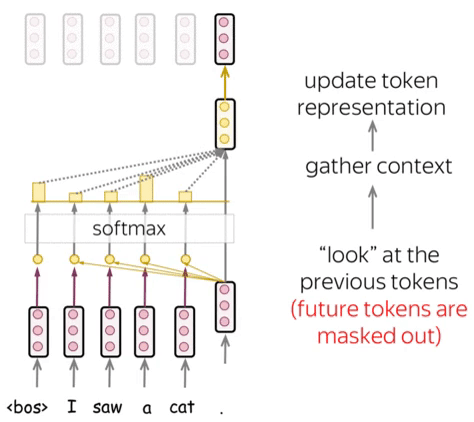
Attention allows the model to focus on relevant parts of the input sequence. The scaled dot-product attention is defined as:
\[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V\]Where:
- $Q$ is the query matrix
- $K$ is the key matrix
- $V$ is the value matrix
- $d_k$ is the dimension of the keys
Attention enables language models to focus on crucial parts of a sentence, considering context. This allows them to grasp complex language, long-range connections, and word ambiguity.
Multi-Head Attention Implementation:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class MultiHeadAttention(nn.Module):
def __init__(self, d_model, num_heads):
super(MultiHeadAttention, self).__init__()
self.num_heads = num_heads
self.d_model = d_model
assert d_model % num_heads == 0
self.d_k = d_model // num_heads
self.W_q = nn.Linear(d_model, d_model)
self.W_k = nn.Linear(d_model, d_model)
self.W_v = nn.Linear(d_model, d_model)
self.W_o = nn.Linear(d_model, d_model)
def scaled_dot_product_attention(self, Q, K, V, mask=None):
attn_scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_k)
if mask is not None:
attn_scores = attn_scores.masked_fill(mask == 0, -1e9)
attn_probs = F.softmax(attn_scores, dim=-1)
output = torch.matmul(attn_probs, V)
return output
def forward(self, Q, K, V, mask=None):
batch_size = Q.size(0)
# Linear projections
Q = self.W_q(Q).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
K = self.W_k(K).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
V = self.W_v(V).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
# Apply attention on all the projected vectors in batch
x = self.scaled_dot_product_attention(Q, K, V, mask)
# Concatenate and apply final linear layer
x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.d_model)
return self.W_o(x)
Text Preprocessing Operations
Let me explain each of these text processing concepts in simple terms:
1. Cleaning:
- Removing special characters: Getting rid of
@#$%, punctuation marks, emojis, etc.1
text = text.replace('@#$%', '') # Basic example
- Handling case sensitivity: Making all text either lowercase or uppercase so “Hello” and “hello” are treated the same
1
text = text.lower() # Convert to lowercase
- Removing stop words: Eliminating common words like “the”, “is”, “at” that don’t add much meaning
1 2 3
from nltk.corpus import stopwords stop_words = set(stopwords.words('english')) text = [word for word in text if word not in stop_words]
2. Normalization:
- Lemmatization: Converting words to their dictionary base form
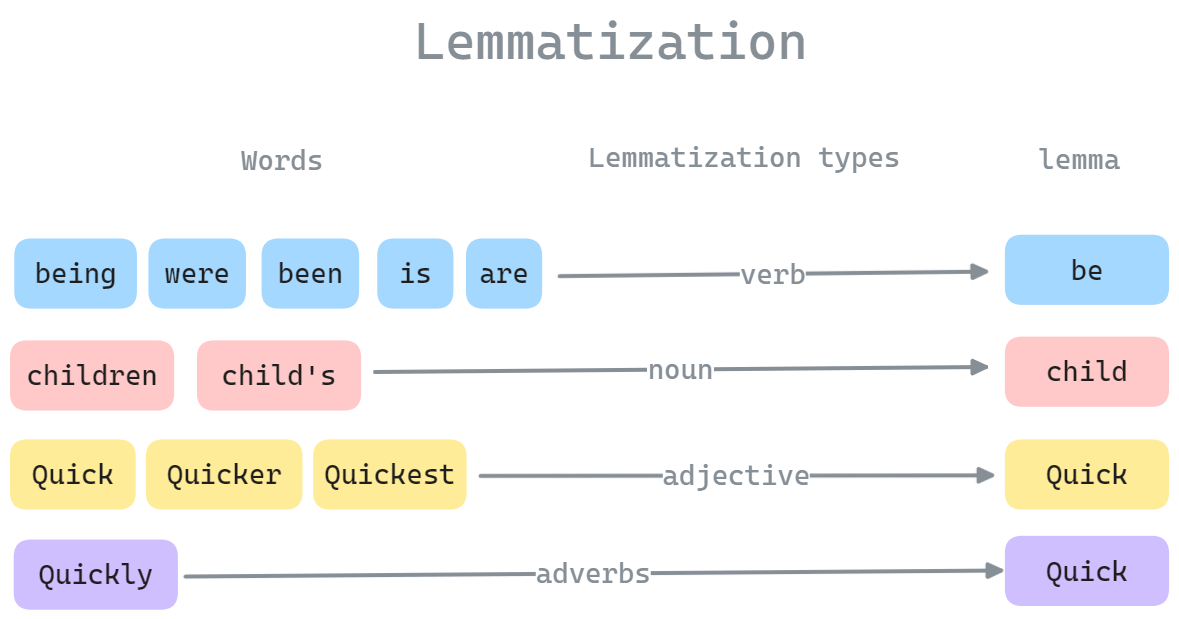
 Figure 2.0: Lemmatization process
Figure 2.0: Lemmatization process
1
2
3
from nltk.stem import WordNetLemmatizer
lemmatizer = WordNetLemmatizer()
word = lemmatizer.lemmatize("running") # Returns "run"
- Stemming: Cutting off word endings to get a common base (faster but rougher than lemmatization)
1
2
3
from nltk.stem import PorterStemmer
stemmer = PorterStemmer()
word = stemmer.stem("fishing") # Returns "fish"
- Unicode normalization: Making sure similar characters are treated the same
- “café” and “café” look same but might use different encodings
1 2
import unicodedata text = unicodedata.normalize('NFKD', text)
- “café” and “café” look same but might use different encodings
These steps help prepare text data for analysis by making it more consistent and removing noise.
Advanced Text Operations
Text Augmentation
Text augmentation techniques help increase dataset size and improve model robustness:
Synonym Replacement: Replace words with their synonyms
Back Translation: Translate text to another language and back
Random Insertion/Deletion: Randomly insert or delete words while preserving meaning
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def synonym_replacement(text, n=1):
words = text.split()
new_words = words.copy()
random_word_list = list(set([word for word in words]))
num_replaced = 0
for random_word in random_word_list:
synonyms = []
for syn in wordnet.synsets(random_word):
for l in syn.lemmas():
synonyms.append(l.name())
if len(synonyms) >= 1:
synonym = random.choice(list(set(synonyms)))
new_words = [synonym if word == random_word else word for word in new_words]
num_replaced += 1
if num_replaced >= n:
break
return ' '.join(new_words)
Sequence Padding
To handle variable-length sequences in batches, padding is used to make all sequences the same length:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def pad_sequences(sequences, max_len=None, padding='post'):
if max_len is None:
max_len = max(len(seq) for seq in sequences)
padded_sequences = []
for seq in sequences:
if len(seq) < max_len:
if padding == 'post':
padded_seq = seq + [0] * (max_len - len(seq))
else: # pre-padding
padded_seq = [0] * (max_len - len(seq)) + seq
else:
padded_seq = seq[:max_len]
padded_sequences.append(padded_seq)
return torch.tensor(padded_sequences)
Reference: